Practical use case: Distance sensor (PoC)
- Ivaylo Fiziev
- Dec 9, 2024
- 4 min read
Updated: Jan 27, 2025

How do we check if the position of a 3D point is above or below a given 3D plane? This is a classic math problem and it has a well known solution - vectors. The reason I am emphasizing on it here is because this calculation is often used in virtual sensors.
Imagine that you have a part appearance and a part sensor that should detect it regardless of its orientation in space. Leaving aside the details behind getting the part appearance location (this is still a work in progress), we need a way to check if this location is above the plane the sensor is currently positioned in. If it is then we can surely say that the part is being detected by the sensor. If the part is behind the sensor's plane we can surely say that the sensor does not see the part. This will be the case for an idealistic ultrasonic sensor with 180 deg field of view. In the real case distance sensors need to check not only the distance to the part but also if the part falls within their field of view. Now how do we achieve this with SCL? As already mentioned we need 3D vectors for this to work.
Let's begin with the definition of a vector in 3D space. It is just a 3D point:
TYPE "VEC_3D"
VERSION:1.0
STRUCT
X:LREAL;
Y:LREAL;
Z:LREAL;
END_STRUCT;
END_TYPENext we need the definition of a 3D plane. By definition a plane is defined by three points (vectors):
TYPE "PLANE_3D"
VERSION:1.0
STRUCT
POINTS: Array[1..3] of "VEC_3D";
END_STRUCT;
END_TYPEEasy stuff. Isn't it? Now we need a way to create a plane based on the sensor's location in space. For this we rely on the OFFSET_ABS_LOC function to find three points of the plane:
FUNCTION "GET_PLANE_FROM_LOC" : VOID
VAR_INPUT
PX : LREAL; // offset along the X axis for the first point
PY : LREAL; // offset along the Y axis for the second point
PZ : LREAL; // offset along the Z axis for the third point
END_VAR
VAR_IN_OUT
LOC:"ABS_LOC"; // sensor's location
END_VAR
VAR_OUTPUT
PLN:"PLANE_3D"; // the plane
END_VAR
VAR_TEMP
locArr:Array[1..3] of "ABS_LOC";
END_VAR
BEGIN
// calculate plane points
OFFSET_ABS_LOC(IN:=#LOC, X:=#PX, OUT=>#locArr[1]);
OFFSET_ABS_LOC(IN:=#LOC, Y:=#PY, OUT=>#locArr[2]);
OFFSET_ABS_LOC(IN:=#LOC, Z:=#PZ, OUT=>#locArr[3]);
// return plane points
#PLN.POINTS[1].X := #locArr[1].x;
#PLN.POINTS[1].Y := #locArr[1].y;
#PLN.POINTS[1].Z := #locArr[1].z;
#PLN.POINTS[2].X := #locArr[2].x;
#PLN.POINTS[2].Y := #locArr[2].y;
#PLN.POINTS[2].Z := #locArr[2].z;
#PLN.POINTS[3].X := #locArr[3].x;
#PLN.POINTS[3].Y := #locArr[3].y;
#PLN.POINTS[3].Z := #locArr[3].z;
END_FUNCTIONOnce we have the plane we need to get its normal vector. The normal vector determines the positive detection direction of the sensor. To calculate the normal vector we use vector subtraction, normalization and cross product functions. Basically we calculate the cross product of two normalized vectors on the plane.
FUNCTION "GET_PLANE_NORMAL_VEC" : VOID
VAR_IN_OUT
PLN:"PLANE_3D"; // the plane
END_VAR
VAR_OUTPUT
N:"VEC_3D"; // the normal vector
END_VAR
VAR_TEMP
A:"VEC_3D"; // first vector on the plane
B:"VEC_3D"; // second vector on the plane
END_VAR
BEGIN
"VEC_3D_SUB"(A:=#PLN.POINTS[2], B:=#PLN.POINTS[1], C=>#A);
"VEC_3D_SUB"(A:=#PLN.POINTS[3], B:=#PLN.POINTS[1], C=>#B);
"VEC_3D_NORM"(#A);
"VEC_3D_NORM"(#B);
"VEC_3D_CROSS_PROD"(A:=#A, B:=#B, C=>#N);
END_FUNCTIONFUNCTION "VEC_3D_SUB" : VOID
VAR_IN_OUT
A:"VEC_3D"; // first vector
B:"VEC_3D"; // second vector
END_VAR
VAR_OUTPUT
C:"VEC_3D"; // result
END_VAR
BEGIN
#C.X := #A.X - #B.X;
#C.Y := #A.Y - #B.Y;
#C.Z := #A.Z - #B.Z;
END_FUNCTIONFUNCTION "VEC_3D_NORM" : VOID
VAR_IN_OUT
V:"VEC_3D"; // the vector to normalize
END_VAR
VAR_TEMP
M : LREAL;
END_VAR
BEGIN
#M := SQRT(#V.X * #V.X + #V.Y * #V.Y + #V.Z * #V.Z);
#V.X := #V.X / #M;
#V.Y := #V.Y / #M;
#V.Z := #V.Z / #M;
END_FUNCTIONFUNCTION "VEC_3D_CROSS_PROD" : VOID
VAR_IN_OUT
A:"VEC_3D"; // first vector
B:"VEC_3D"; // second vector
END_VAR
VAR_OUTPUT
C:"VEC_3D"; // result
END_VAR
BEGIN
#C.X := #A.Y * #B.Z - #A.Z * #B.Y;
#C.Y := #A.Z * #B.X - #A.X * #B.Z;
#C.Z := #A.X * #B.Y - #A.Y * #B.X;
END_FUNCTIONFUNCTION "VEC_3D_DOT_PROD" : LREAL
VAR_IN_OUT
A:"VEC_3D";
B:"VEC_3D";
END_VAR
BEGIN
#VEC_3D_DOT_PROD := #A.X * #B.X + #A.Y * #B.Y + #A.Z * #B.Z;
END_FUNCTIONNow we have the primitives needed for our calculation. What is left is to use these functions in the block of the sensor. The code has to do a number of steps:
get the location of the detected part appearance (TBD)
get the location of the sensor
get the sensor's plane and normal vector (normalized)
find a vector from the part location to a point on the plane and normalize it
calculate the dot product of this vector and the normal vector of the plane
positive result indicates that the part is located in front of the sensor. negative result indicates that the part is located behind the sensor
analyze the angle between the normal vector and the vector to the part. this angle gives us the field of view of the sensor.
in case the angle is within the sensor's range calculate the distance to the part
The code snippet below is not fully functional since we are still missing (at least
officially) the function to get the appearance location. The rest however is valid for any similar use cases. I am using a picture since wix.com crashed a few times on me when pasting the text. Shame!
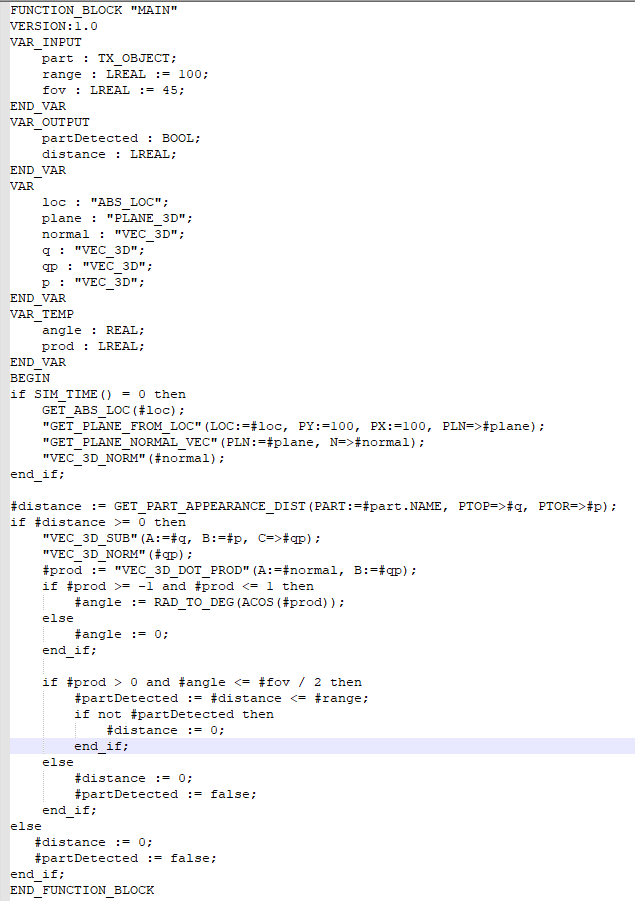
Instead of the part location we can rely on the point of minimal distance to the sensor.
In this case however we should consider that the part geometry might affect the measurements. With irregular shapes the angle between vectors might often get out of the fields of view of the sensor. In this case it is recommended to use a wider field of view.
In v2502 we have feature toggle (SCL_DISTANCE_SENSOR) that enables the functions for getting the part appearance location / minimal distance so you can try it.
It is a POC but works perfectly well in dev environment. We plan to release the FT function and also provide built-in functions for vector calculations. The concept however will remain the same. Just with better performance.
Enjoy it!
Update 1: The code for the sensor assumes that the sensor does not change its orientation in space. This is why it only calculates the plane's normal vector once at the beginning of the simulation. If the sensor rotates its plane during simulation then you should detect this condition and re-calculate the normal vector. e.g.




Comments